Ejemplo didáctico 2.

En la lección anterior vinculamos algunos fenómenos periódicos de la naturaleza, como los ciclos de la luna, con la obtención de señales discretas para representar la periodicidad de dicho fenómeno. Ahora partiremos directamente de una señal analógica, como puede ser una señal de audio que viaja por un cable. 

Realizaremos los procesos de muestreo y cuantización de una conversión Analógico/Digital .

Preámbulo.

- La digitalización, ¿es un proceso destructivo?

- No, siempre y cuando se realice “apropiadamente”.  

El teorema de muestreo:

"La definición del muestreo apropiado es relativamente sencilla. Supón que, de alguna manera, realizas el muestreo una señal continua. Si eres capaz de reconstruir la señal analógica a partir de estas muestras, eso significa que has realizado el muestreo de forma apropiada. Incluso si los datos muestreados son aparentemente confusos o incompletos, la información clave ha sido capturada si puedes revertir el proceso."   

(extraído y traducido de la DSP Guide, capitulo 3)

Preguntas:

¿Cuál es el rango de frecuencias audibles por el oído humano?

¿Qué rango de frecuencias puedo representar con las siguientes frecuencias de muestreo y cuáles cubren todo el rango audible por el oído humano?

22.050 Hz

44100 Hz

96000 Hz

A los efectos didácticos de comprender el proceso de digitalización, se suele dividir en dos etapas;

-1 Muestreo 

-2 Cuantización.

Imaginemos que conectamos un micrófono a la entrada de una interfaz que pre-amplifica y convierte audio analógico en audio digital. Las variaciones de presión captadas por el micrófono serán transducidas como variaciones de voltaje en el tiempo, generando, a la salida del micrófono, una señal eléctrica de voltaje variable, análoga a las variaciones de presión en aire.

 

De esta forma 0 volts equivaldrá al nivel de presión atmosférica y será el eje de nuestra representación. La amplitud de la señal dependerá de cuanto pueda amplificarla antes de la conversión, sin que llegue a los niveles de saturación del sistema. A su vez, en el eje x tendremos la variable tiempo. Nuestra señal analógica de partida, se caracteriza por ser un voltaje que varía en función del tiempo. 

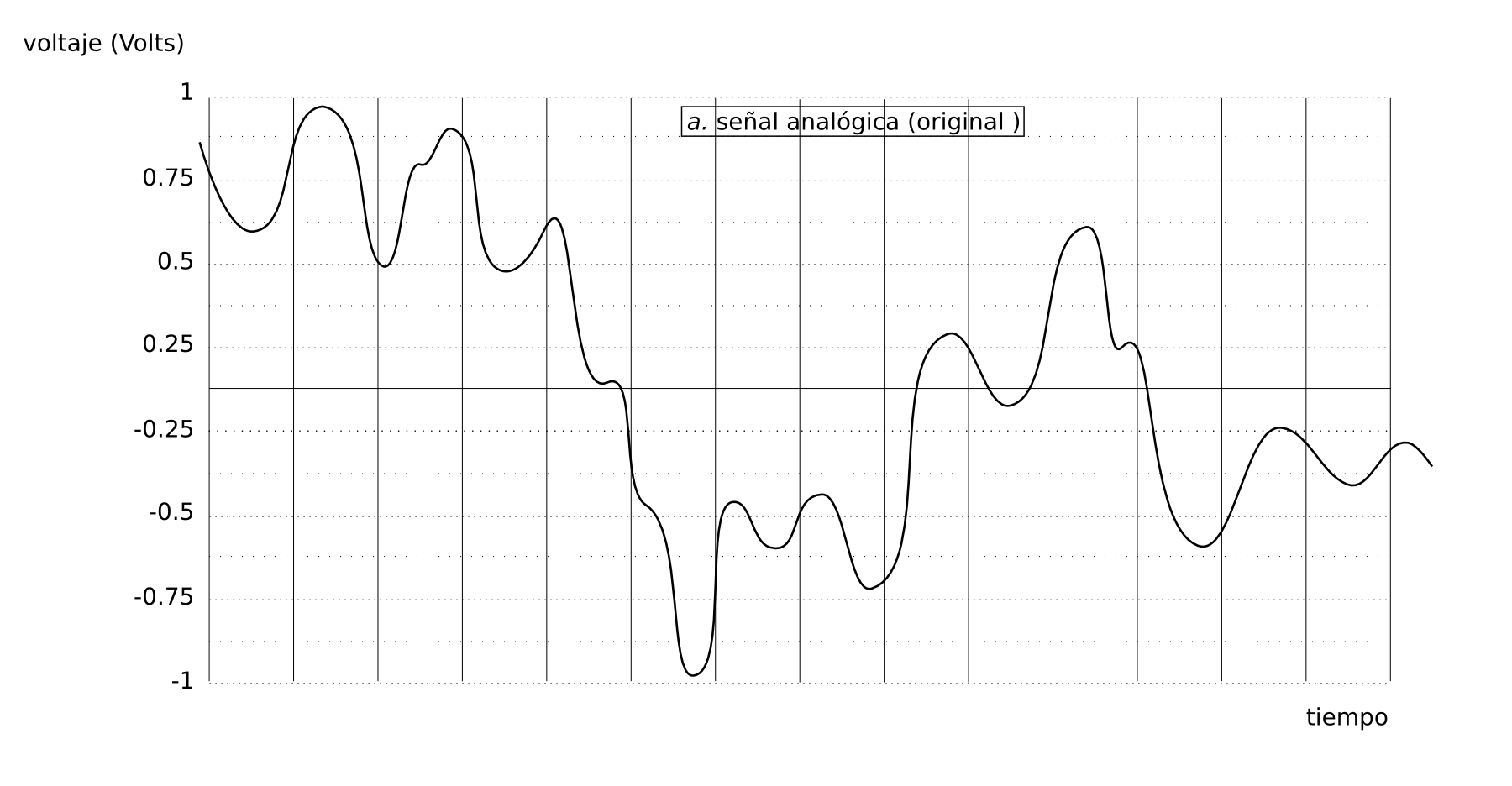
(imagen a. señal analógica)

1 Muestreo o "sampling and hold".

En el proceso de muestreo, el tiempo deja de ser una variable continua y se define como una suma de instantes temporales a una distancia igual. La distancia entre muestras estará definida por la frecuencia de muestreo, comúnmente denominada fs, por su nombre en inglés "sample frecuency” o “sample rate". Por ejemplo, para fs = 44.100Hz el período de muestreo, Ts, (distancia entre muestras) es igual al inverso de la frecuencia de muestreo, fs. Ts = 1 / 44100 = 0,000022676 seg.

La distancia temporal entre muestras (Ts)  es inversamente proporcional a la frecuencia de muestreo, fs, por ende al aumentar la frecuencia de muestreo, la distancia temporal entre muestras es menor, lo que resulta en un aumento de la resolución temporal de la señal.

"La señal resultante solo podrá cambiar a intervalos periódicos (Ts), para cada muestra el valor es idéntico al valor instantáneo de la señal de entrada. Cambios en la señal entrante que sucedan entre estos intervalos de tiempo serán completamente ignorados. Entonces, el proceso de Muestreo convierte la variable independiente (en este caso el tiempo) de continua a discreta." (traducción de la DSP Guide)

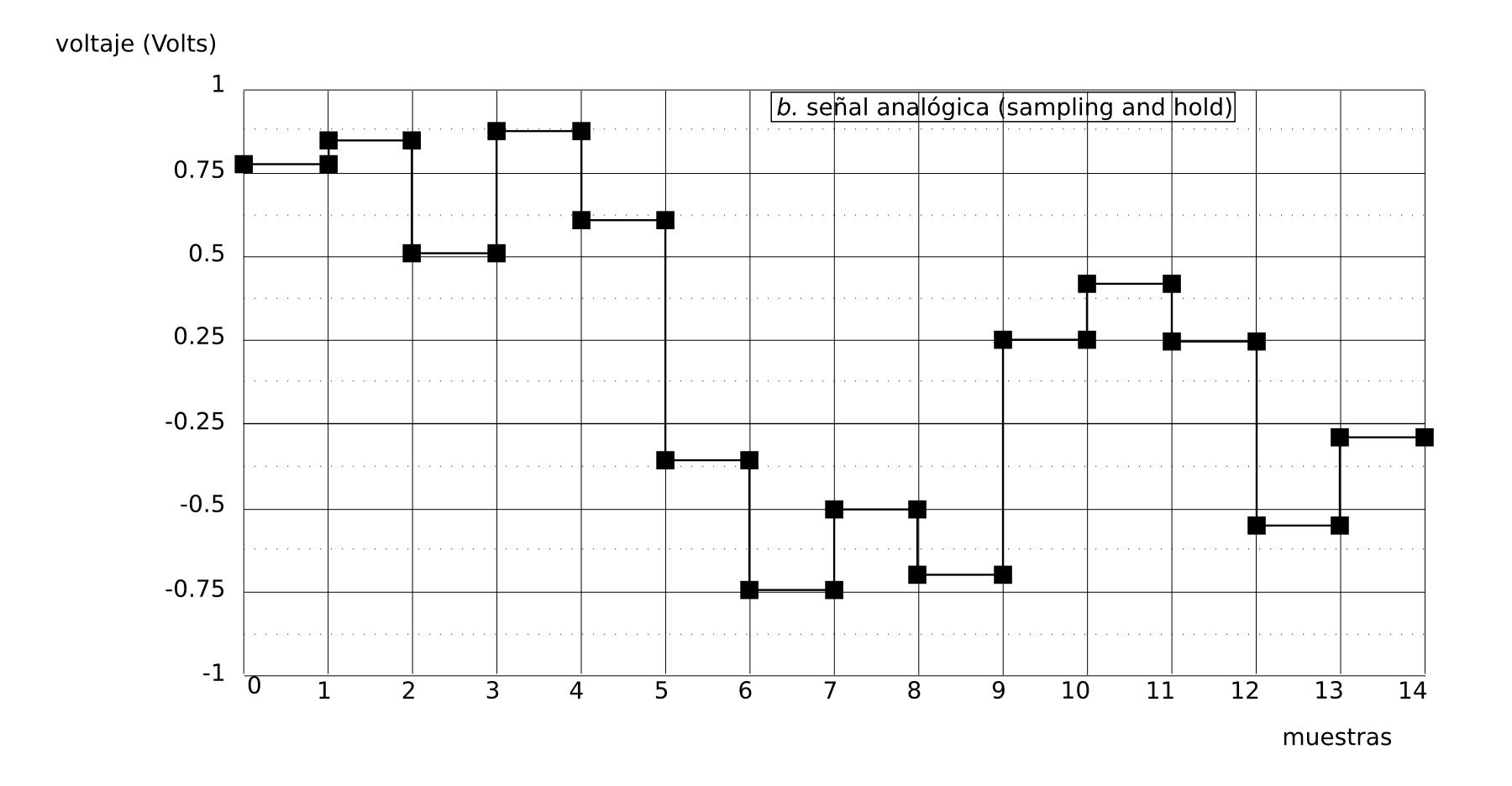
(imagen b. señal analógica)

2 Cuantización y ruido de cuantización

En este proceso, la variable amplitud (en este caso el voltaje) se convierte de continua a discreta. El voltaje se transforma a valores de amplitud digitales. Imaginemos que la señal de audio es, dentro de una computadora, una serie de valores numéricos ordenados con un índice. El índice es el numero de muestra o eje x. Mientras que por cada una de estas muestras existe una palabra compuesta por una serie de caracteres binarios. De esta forma, si la resolución que tenemos para representar la amplitud es de 3Bits, por cada muestra tendremos 2³ = 8 posibles valores. Es decir que el valor instantáneo de voltaje que toma la señal para cada muestra se aproximará a el valor más cercano dentro de las posibilidades que me da dividir la amplitud en 8 partes iguales.

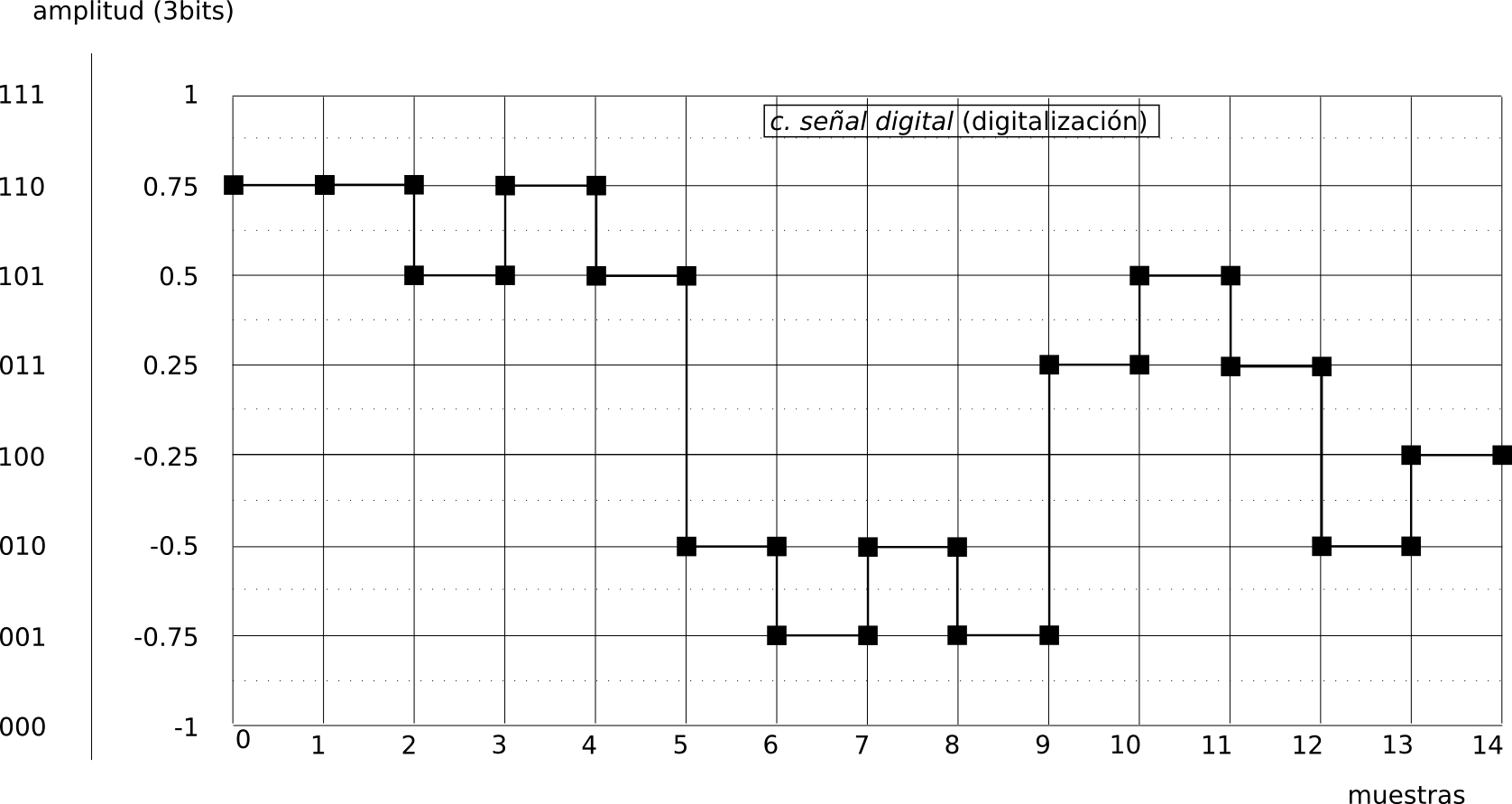
(imagen c)

Las líneas horizontales marcan los valores posibles a una resolución de 3Bits. Es decir, que la amplitud, se ajustará a esta grilla de 8 posibilidades.

Las líneas punteadas horizontales muestran el punto medio entre dos valores distintos, esto facilita la aproximación de la amplitud al valor posible más cercano, ya sea el superior si está por encima de la linea punteada, o el inferior si está por debajo de la línea punteada.

Veamos el resultado de la cuantización en la "señal c" y analicemos en qué se diferencia con la "señal b"

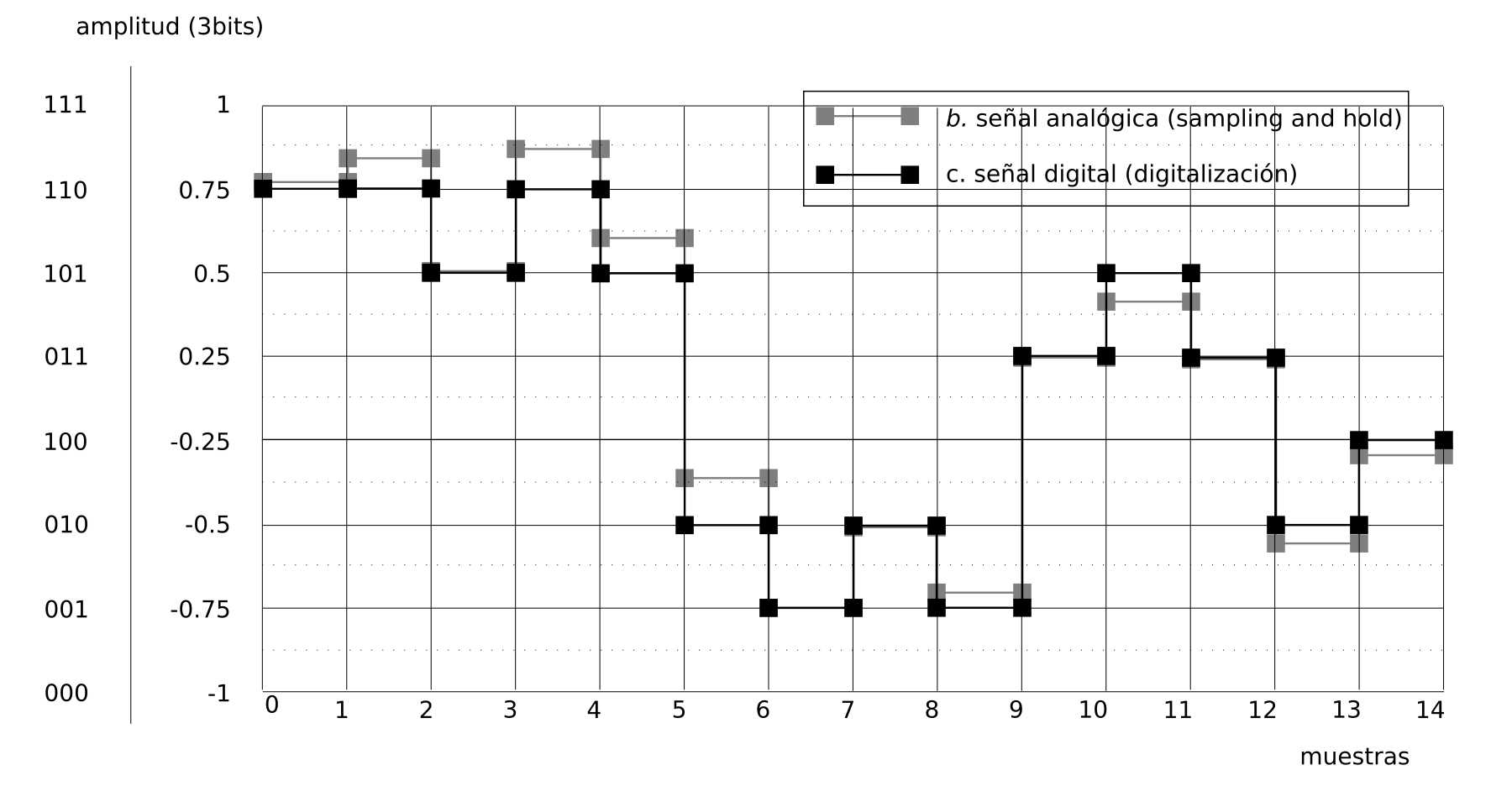
(imagen b y c)

En el gráfico se muestra claramente la diferencia entre las señales b y c. Siendo que en el eje y la "señal b" es continua y la "señal c" discreta con solo 3bits de resolución.

Cada vez que movemos un valor al bit más cercano es como si estuviéramos sumando un cierto valor (positivo o negativo) a la señal b. Se podría decir que la señal c (cuantizada) se obtiene producto de sumar una cierta cantidad de ruido a la señal b. Podemos afirmar que esta señal es ruido por probabilidad.

Anotaremos el valor aproximado de voltaje que fue necesario sumar para que cada muestra se ajustase a los 3bits de resolución. Graficamos este valor y obtenemos la señal que corresponde al ruido de cuantización.

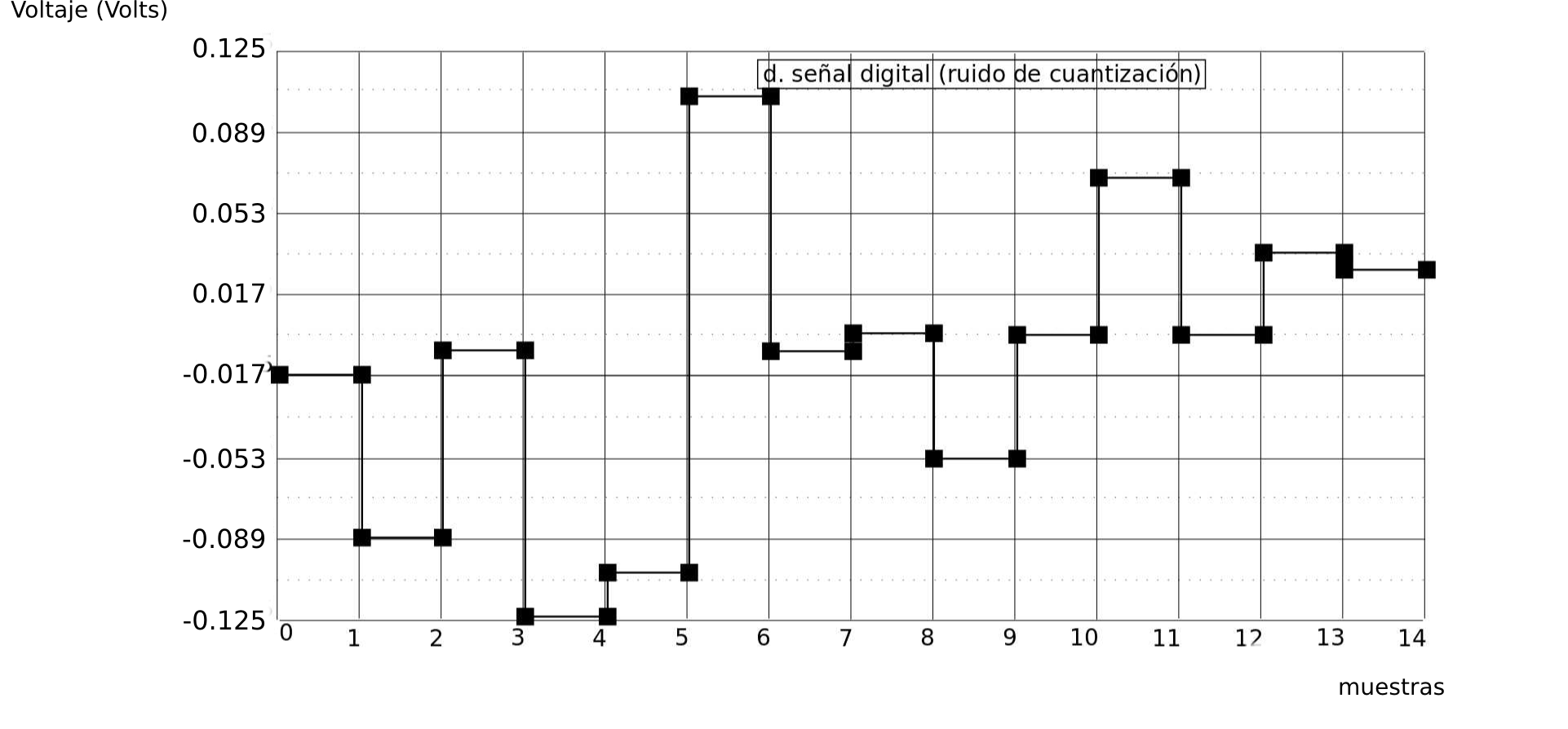
(imagen d. ruido de cuantización)

El ruido de cuantización es intrínseco al proceso de convertir la amplitud de una señal de continua a discreta. Si aumentamos el nº de bits de resolución, la diferencia entre el valor continuo y el discreto será mucho menor, generando niveles de ruido mucho más bajos. Hoy en día los conversores de audio digital alcanzan los 24bits, lo que da una resolución de 2²⁴ posibles valores.