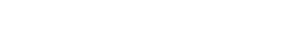Cómo obtener una señal digital de la naturaleza

conceptos nuevos: -frecuencia -período 

Introducción al ejemplo

Para comprender de una forma intuitiva el proceso de conversión analógico/digital, imaginemos que queremos obtener una señal de valores discretos, que represente un fenómeno natural cualquiera, en este caso tomaremos como ejemplo los ciclos o fases de la luna. 

La señal que deseamos obtener es aquella que describe el denominado "fenómeno de lunación" en dos de sus dimensiones; el tiempo y el espacio. El tiempo que le toma a la luna llegar a una misma posición relativa al planeta tierra y el sol. Este fenómeno se da, como sabemos, en aproximadamente 30 días. A este ciclo se le denomina "lunación" y es el tiempo que pasa, por ejemplo, entre que vemos una luna llena y la siguiente.

En la animación se muestra, de forma acelerada, cómo varía nuestra fuente de una forma, digamos continua, en el tiempo. Cada vez que se cumple un ciclo entero significa que han trascurrido 30 días:

Dicho fenómeno tiene un período de lunación "T" igual a 30 días y una frecuencia de lunación "f ".

Sobre el período y la frecuencia del fenómeno.

La función que vincula período y frecuencia es la de proporcionalidad inversa. Es decir que al aumentar la frecuencia disminuye el período.

En otras palabras, si el movimiento relativo de estos astros fuera más veloz, aumentaría la frecuencia. Por lo tanto el período, definido como el tiempo transcurrido entre que la luna alcanza la misma posición relativa al sol y la tierra, sería más corto.

Lo mismo expresado matemáticamente sería:

f = 1 / T              o bien: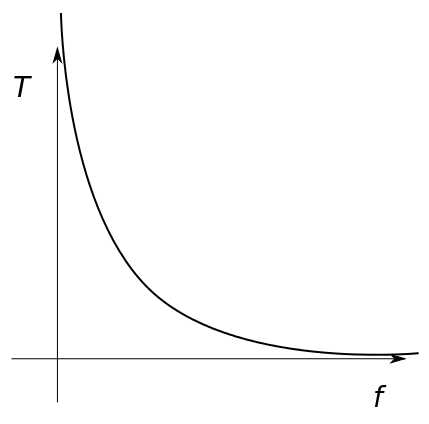                        

Ejercicio 1: Dado el "período de lunación", cuál sería el valor de la "frecuencia de lunación".

-----------------------------------------------------------------------------------------------------------------------------

Representación gráfica

Para obtener una señal que represente dicho período, debemos tomar muestras cada cierto intervalo de tiempo. Estas muestras, como veremos en el siguiente cuadro, pueden estar asociadas a una imagen. La señal debe estar representada numéricamente, para el uso del DSP. Por ello cada una de estas imágenes se traduce o a un valor de amplitud genérico. Establecimos el valor -1 para la luna nueva y 1 para la luna llena.

Si el estudiante es atento, notará que algunas posiciones simétricas como las de las muestras 1 y 7 llevan un mismo valor de amplitud. Esa información está relacionada a la fase de la oscilación y lo dejaremos de lado por ahora.

¿Por qué asociar las imágenes a un valor de amplitud de este tipo?

En primer lugar, asociamos cada imagen a un valor de amplitud con la finalidad de poder obtener una señal en dos ejes, x (variable independiente) e y (variable dependiente). 

En segundo lugar, la representación de señales con valores de amplitud "normalizados" entre 1 y -1 es utilizada comúnmente por editores de audio, sintetizadores digitales, visualizadores de audio digital, etc. Con el fin emparentar este ejemplo a una señal de audio, establecimos el valor -1 para la luna nueva y 1 para la luna llena, como se mencionaba anteriormente.

El siguiente cuadro muestra las imágenes obtenidas de la luna, a intervalos de tiempo iguales a 1 octavo del período de lunación. Es decir, cada 30/8 días. Cada muestra está numerada naturalmente para ordenar los datos en una cadena. La última fila del cuadro contiene los valores de amplitud normalizados para cada una de las muestras tomadas: 

Cuadro 1: muestras de las fases de la luna tomadas cada 1/8 del período completo de lunación. Cada período está representado por 8 muestras equidistantes en el tiempo.

Si representamos los valores de amplitud en una gráfica, podemos visualizar la siguiente señal periódica:

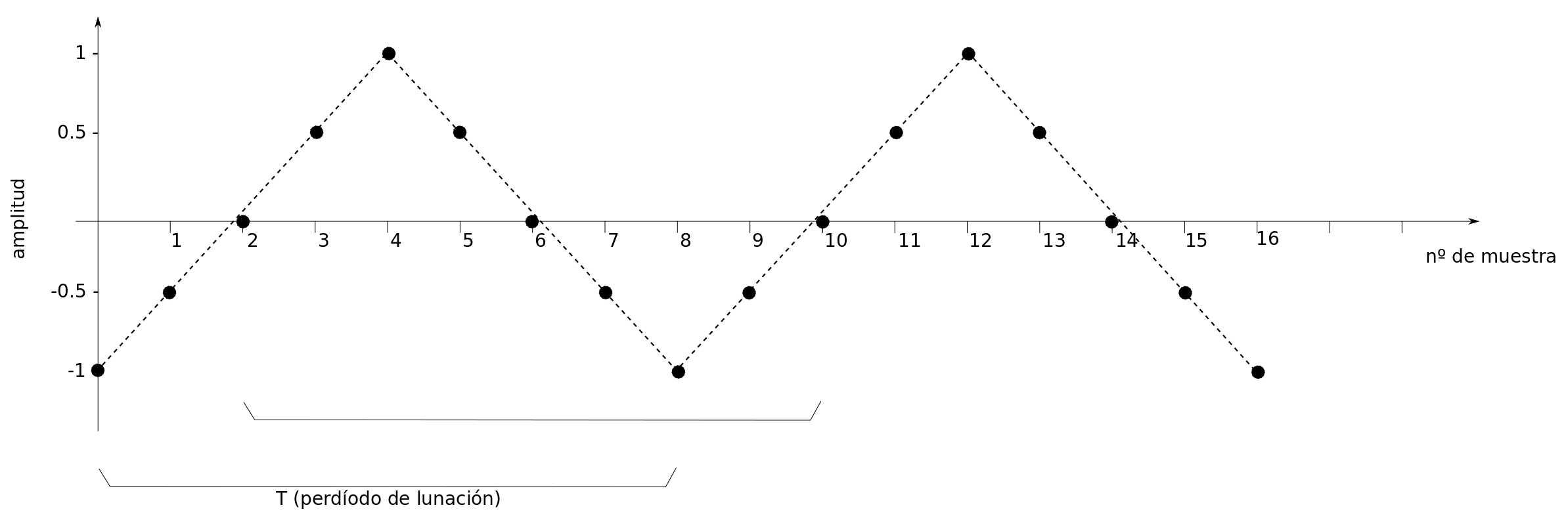
Gráfico 1: En el eje y está representada la variable dependiente o amplitud. En el eje x está representada la variable independiente o nº de muestra. La amplitud representa la posición de la luna, según lo descrito en el cuadro 1. El nº de muestra representa las observaciones realizadas cada 1/8 del período de lunación "T". 

---------------------------------------------------------------------------------------------------------------------------------------------

Observaciones de la señal obtenida

1- Dadas las 16 muestras obtenidas, podemos prever el comportamiento de la señal hacia adelante o hacia atrás en el eje x.

2- La línea punteada solo está representada con el fin de clarificar la visualización de la periodicidad de la señal. La señal son los valores discretos para cada muestra. La señal no contiene información entre muestras, aunque en este caso resulte trivial determinar los valores intermedios.

3- El período de la señal está indicado a partir de la muestra 0, pero podría medirse a partir de cualquier muestra. Por ejemplo podríamos medirlo desde la muestra 2 hasta la muestra 10. Es decir, que podemos afirmar que la señal es periódica, por que cada 8 muestras el ciclo se repite idéntico, independientemente de cuál muestra consideremos como la primera del ciclo.

4- La forma de la onda obtenida es triangular, esta forma de onda resulta de un proceso de reducción del objeto de estudio a variables muy simples y lineales, y su representación en este ejemplo es a los fines de visualizar la periodicidad del fenómeno de una forma sencilla. Veremos más adelante que existen otras formas de onda (aleatorias, sinusoidales, cuadradas, así como formas complejas y periódicas al mismo tiempo, etc...).

5- Teniendo en cuenta la información que se desprende de esta primera medición; por ejemplo, que es periódica y que tiene una forma determinada. Vemos que muchas de las muestras que tomamos tienen un alto nivel de redundancia, ya que no aportan información significativa para la comprensión del fenómeno. Retomaremos este punto más adelante, pero parece lógico pensar que cuantas menos muestras tengamos que tomar para describir un fenómeno será más eficiente y económico el proceso de representación, almacenamiento y transmisión de estas señales.

6- La frecuencia a la que se obtienen las muestras, se denomina frecuencia de muestreo y lo abreviaremos como fs (por su nombre en inglés sampling frequency). Esto tiene como finalidad hacer este material más compatible con la nomenclatura que comúnmente se utiliza en entornos de trabajo, manuales de usuario, en la bibliografía, etc. Además de ser la terminología que se utilizará en este curso. 

7- El intervalo temporal entre muestras lo llamaremos en este ejemplo, período de muestreo, y lo abreviaremos como Ts. Nuevamente, estos dos últimos valores se relacionan de forma inversamente proporcional: fs = 1 / Ts.

8- Es importante entender que tanto la "amplitud" como el "nº de muestra" podrían ser sustituidos por otras variables y que la señal resultante siga representando el mismo fenómeno. Por ejemplo utilizar "días" en lugar de "nº de muestra" en el eje x.

Ejercicio 2: Calcule los valores de período y frecuencia de muestreo (Ts y fs) utilizados para obtener la señal del Gráfico 1.

Frecuencias Alias, introducción al teorema de muestreo

Como se menciona en el punto 5 de las observaciones la cantidad de muestras necesarias para representar un fenómeno periódico es un punto importante ya que las señales digitales son discretas y la cantidad de información será determinante en el almacenamiento y velocidad de transmisión. 

¿Cuál es el mínimo de muestras que debo tomar para poder reconstruir la señal original?

En los siguientes ejemplos veremos como al aumentar la distancia entre muestras se puede perder información relevante. Es decir que existe un limite donde el período de lunación no será correctamente representado.

En el ejemplo de arriba, las muestras fueron tomadas cada 1/8 del período del fenómeno. Veamos que sucede si tomamos muestras a intervalos mayores de tiempo: cada 3/8 y cada 5/8 de la duración total del período de lunación. Si el período de lunación es de 30 días, estaremos tomando muestras cada 11,25 días en el primer caso y cada 18,75 días en el segundo. Note que en el primer caso la distancia temporal entre muestras es menor que la mitad del período de lunación Ts, y en el segundo es mayor.

Analicemos los datos desde el punto de vista de la frecuencia:

Ej 1

La frecuencia "f" del fenómeno es 1/(30 días) = 0,0333 ciclos por día

La frecuencia de muestreo "fs₁" es 1/(11.25 días) = 0,0888 ciclos por día

Es decir que: fs₁ > 2f

En el primer caso, las muestras de la luna están a una distancia de 11,25 días, es decir 3/8 de la duración del período de la señal original. La señal resultante es una señal periódica cuyo período se repite 3 veces en un lapso de 90 días. Es decir que el período de esta señal es de 30 días, por lo que concluimos que la señal "lunación" está correctamente representada.

Ej 2

La frecuencia "f" del fenómeno es 1/(30 días) = 0,0333 ciclos por día

La frecuencia de muestreo "fs₂" es 1/(18.75 días) = 0,0533 ciclos por día

Es decir que: fs₂ < 2f

En el segundo caso, sin embargo, las distancias entre muestras son de 18, 75 días, es decir 5/8 de la duración del período de lunación original. La señal resultante es también periódica pero esta se repite 3 veces en un lapso de 150 días. Es decir que el período de esta señal es de 50 días, por lo que concluimos que la señal "lunación" no está debidamente representada.

 

Lo que sucede en el segundo ejemplo es que la frecuencia resultante (igual 1/50) no corresponde con la frecuencia de lunación (igual a 1/30) y lo que se está representando es una frecuencia "alias" que es falsa.

Este problema a la hora de digitalizar señales está resuelto por el teorema de muestreo, que establece que para digitalizar una señal, cuya frecuencia más alta sea f, la frecuencia de muestreo necesaria para poder reconstruir la señal original debe ser mayo a 2f.

El proceso de digitalización del fenómeno lunación, en este caso, no cumple con el teorema de muestreo. Ya que la frecuencia de muestreo fs₂ es menor al doble de la frecuencia que se quiere representar.